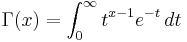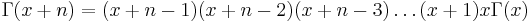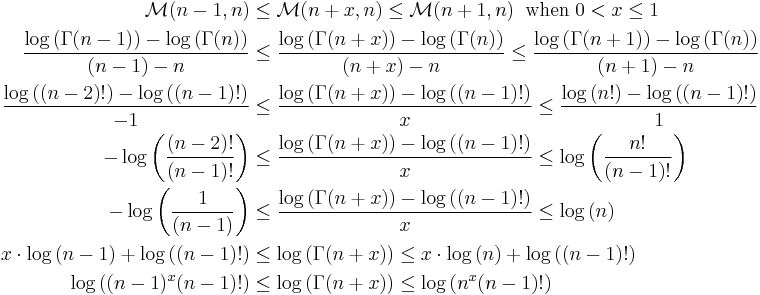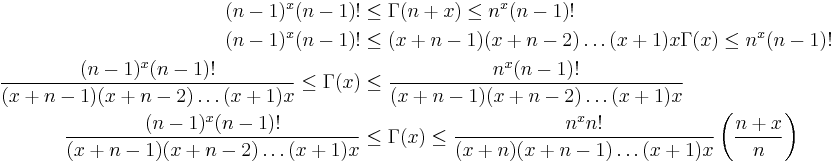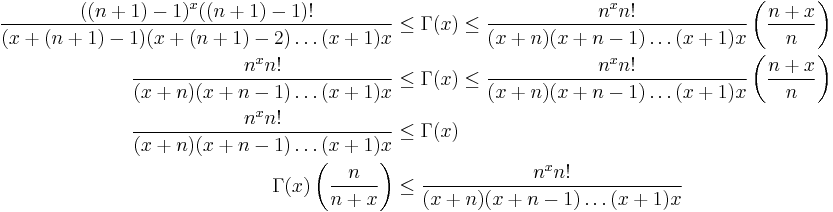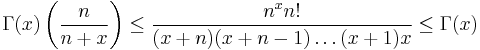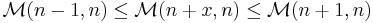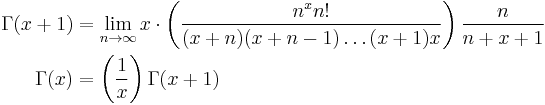Bohr–Mollerup theorem
In mathematical analysis, the Bohr–Mollerup theorem is named after the Danish mathematicians Harald Bohr and Johannes Mollerup, who proved it. The theorem characterizes the gamma function, defined for x > 0 by
as the only function f on the interval x > 0 that simultaneously has the three properties
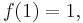 and
and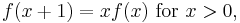 and
and- f is logarithmically convex.
An elegant treatment of this theorem is in Artin's book The Gamma Function, which has been reprinted by the AMS in a collection of Artin's writings.
The theorem was first published in a textbook on complex analysis, as Bohr and Mollerup thought it had already been proved.
Contents |
Proof
Statement of the Theorem
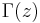 is the only function that satisfies
is the only function that satisfies 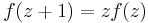 with
with 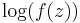 convex and also with
convex and also with 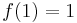 .
.
Proof
Let 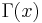 be a function with the assumed properties established above:
be a function with the assumed properties established above: 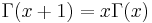 and
and 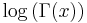 is convex, and
is convex, and 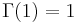 . From the fact that
. From the fact that 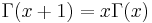 we can establish
we can establish
The purpose of the stipulation that 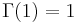 forces the
forces the 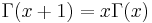 property to duplicate the factorials of the integers so we can conclude now that
property to duplicate the factorials of the integers so we can conclude now that 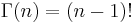 if
if 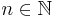 and if
and if 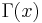 exists at all. Because of our relation for
exists at all. Because of our relation for 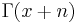 , if we can fully understand
, if we can fully understand 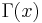 for
for 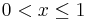 then we understand
then we understand 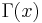 for all values of
for all values of 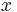 .
.
The slope of a line connecting two points 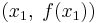 and
and 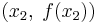 , call it
, call it 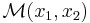 is monotonically increasing for convex functions with
is monotonically increasing for convex functions with 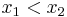 . Since we have stipulated
. Since we have stipulated 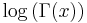 is convex we know
is convex we know
It is evident from this last line that a function is being sandwiched between two expressions, a common analysis technique to prove various things such as the existence of a limit, or convergence. Now we recall that the function  and
and 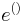 are both monotonically increasing. Therefore if we exponentiate each term of the inequality, we will preserve the inequalities. Continuing:
are both monotonically increasing. Therefore if we exponentiate each term of the inequality, we will preserve the inequalities. Continuing:
The last line is a strong statement. In particular, \textit{it is true for all values of 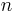 }. That is
}. That is 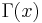 is less than the right hand side for any choice of
is less than the right hand side for any choice of 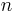 and likewise,
and likewise, 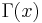 is greater than the left hand side for any other choice of
is greater than the left hand side for any other choice of 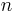 . Each single inequality stands alone and may be interpreted as an independent statement. Because of this fact, we are free to choose different values of
. Each single inequality stands alone and may be interpreted as an independent statement. Because of this fact, we are free to choose different values of 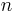 for the RHS and the LHS. In particular, if we keep
for the RHS and the LHS. In particular, if we keep 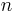 for the RHS and choose
for the RHS and choose 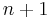 for the LHS and get:
for the LHS and get:
We can combine the last two lines into
Now let 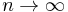 . The limit drives
. The limit drives 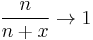 so the left side of the last inequality is driven to equal the right side.
so the left side of the last inequality is driven to equal the right side. 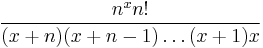 is sandwiched in between. This can only mean that
is sandwiched in between. This can only mean that 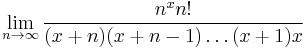 is equal to
is equal to 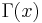 . In the context of this proof this means that
. In the context of this proof this means that 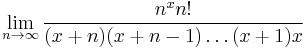 has the three specified properties belonging to
has the three specified properties belonging to 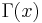 . Also, the proof provides a specific expression for
. Also, the proof provides a specific expression for 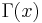 . And the final critical part of the proof is to remember that the limit of a sequence is unique. This means that for any choice of
. And the final critical part of the proof is to remember that the limit of a sequence is unique. This means that for any choice of ![\,x\in(0,1]\,](/2012-wikipedia_en_all_nopic_01_2012/I/f39ac1c88fcf0202afee3b9b2f558277.png) only one possible number
only one possible number 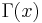 can exist. Therefore there is no other function with all the properties assigned to
can exist. Therefore there is no other function with all the properties assigned to 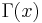 . the assumptions of this theorem to
. the assumptions of this theorem to
The remaining loose end is the question of proving that 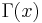 makes sense for all
makes sense for all 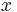 where
where 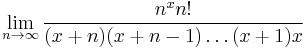 exists. The problem is that our first double inequality
exists. The problem is that our first double inequality
was constructed with the constraint 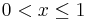 . If, say,
. If, say, 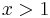 then the fact that
then the fact that  is monotonically increasing would make
is monotonically increasing would make 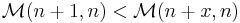 , contradicting the inequality upon which the entire proof is constructed. But notice
, contradicting the inequality upon which the entire proof is constructed. But notice
which demonstrates how to bootstrap 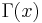 to all values of
to all values of 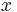 where the limit is defined.
where the limit is defined.
References
- Weisstein, Eric W., "Bohr–Mollerup Theorem" from MathWorld.
- Proof of Bohr–Mollerup theorem on PlanetMath
- Alternative proof of Bohr–Mollerup theorem on PlanetMath
- Artin, Emil (1964). The Gamma Function. Holt, Rinehart, Winston.
- Rosen, Michael (2006). Exposition by Emil Artin: A Selection. American Mathematical Society.
- Mollerup, J., Bohr, H. (1922). Lærebog i Kompleks Analyse vol. III, Copenhagen. (Textbook in Complex Analysis)